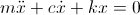1. Introduction
Eigen values physically indicate the natural frequencies of a vibratory system. Depending upon the damping in the system one could obtain pureply imaginary, real or complex eigen values. This brief write up attempts to explain the physical interpretation of imaginary,real or complex eigen values obtained upon solving the equation of motion.
2. Imaginary, real, complex eigen values
The equation of motion of an undamped free vibation is given by;
which admits solution of the form;
where, lambda are the eigen values
Here,
lambda can be obtained as;
which means that ;
lambda is always imaginary since both k and m are always real and positive.
For an undamped, free oscillation, the eigenvalues are always purely imaginary. That means without the damping force, the oscillation will continue into infinity.
Now, for damping the governing equation is
which has the same general form of the solution, only the eigenvalues are now:
In this case, the eigenvalues are purely imaginary if c=0 ;
and the eigen values are real if;
and and are complex if ;
A purely imaginary eigenvalue means the system oscillates for all time (undamped free vibration).
A purely real eigenvalue means that the solutions are exponential and decay directly to zero (since it is impossible to have a positive eigenvalue)- indicating that the system will not oscilllate.
A complex eigenvalue means you have an oscillation of decreasing amplitude until eventually you reach zero.
3. Ways of defining eigen values
There are infact two different ways to define "the eigenvalues" here.
If you are doing vibration analysis of a system without damping, you "know" the response is going to be an oscillation, so instead of what is described above in section 2, that is:
one can normally starts with (as it is in most of the texts on Structural Dynamics);
The first one gives you an imaginary value of lambda , the second gives a real value of omega.
If you have a general damping matrix, you would normally follow the first math (of section 2) which leads to a quadratic eigenproblem. On the other hand if you assume a special forms of damping matrix (e.g. Rayleigh damping) it can be shown that the damped mode shapes are the same as the undamped, so you usually formulate the math in terms of the real values of .omega.
Eigen values physically indicate the natural frequencies of a vibratory system. Depending upon the damping in the system one could obtain pureply imaginary, real or complex eigen values. This brief write up attempts to explain the physical interpretation of imaginary,real or complex eigen values obtained upon solving the equation of motion.
2. Imaginary, real, complex eigen values
The equation of motion of an undamped free vibation is given by;
which admits solution of the form;
where, lambda are the eigen values
Here,
lambda can be obtained as;
which means that ;
lambda is always imaginary since both k and m are always real and positive.
For an undamped, free oscillation, the eigenvalues are always purely imaginary. That means without the damping force, the oscillation will continue into infinity.
Now, for damping the governing equation is
which has the same general form of the solution, only the eigenvalues are now:
In this case, the eigenvalues are purely imaginary if c=0 ;
and the eigen values are real if;
and and are complex if ;
A purely imaginary eigenvalue means the system oscillates for all time (undamped free vibration).
A purely real eigenvalue means that the solutions are exponential and decay directly to zero (since it is impossible to have a positive eigenvalue)- indicating that the system will not oscilllate.
A complex eigenvalue means you have an oscillation of decreasing amplitude until eventually you reach zero.
3. Ways of defining eigen values
There are infact two different ways to define "the eigenvalues" here.
If you are doing vibration analysis of a system without damping, you "know" the response is going to be an oscillation, so instead of what is described above in section 2, that is:
one can normally starts with (as it is in most of the texts on Structural Dynamics);
The first one gives you an imaginary value of lambda , the second gives a real value of omega.
If you have a general damping matrix, you would normally follow the first math (of section 2) which leads to a quadratic eigenproblem. On the other hand if you assume a special forms of damping matrix (e.g. Rayleigh damping) it can be shown that the damped mode shapes are the same as the undamped, so you usually formulate the math in terms of the real values of .omega.